你有没有想过,在数学的世界里,有时候把复杂的问题简化竟然能变得如此有趣?今天,咱们就来聊聊MATLAB中的对数函数,这个既能让你在数据处理中如鱼得水的神器,又能让你的数学问题变得简单到飞起!
对数函数:数学世界的“魔法师”
想象你手里有一堆数字,它们像小山一样高,你想要在图表上展示出来,可是一看,全都是密密麻麻的数字,根本看不清楚。这时候,对数函数就像一位魔法师,轻轻一挥,就能把这些数字变成一个个小矮人,让你轻松看个明白。
在MATLAB里,对数函数主要有三个:`log`、`log10`和`log2`。它们分别对应自然对数、常用对数和以2为底的对数。是不是觉得有点眼花缭乱?别急,咱们一步步来。
自然对数:宇宙的奥秘
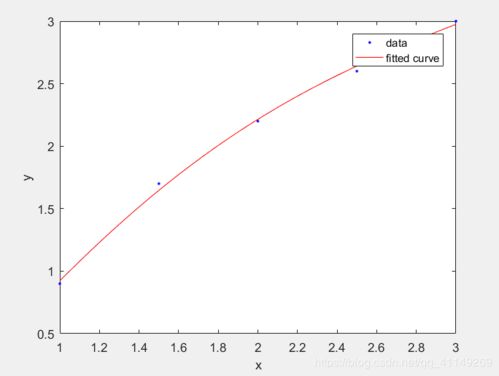
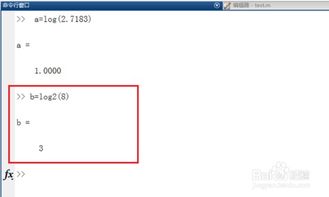
`log`函数,也就是自然对数,它是数学中最基本的对数形式。在MATLAB中,计算一个数的自然对数,只需要简单地在命令窗口输入`log(x)`即可。比如,你想知道e(自然对数的底数,约等于2.71828)的自然对数是多少,直接输入`log(exp(1))`,MATLAB就会告诉你答案是1。
自然对数在科学研究中有着广泛的应用,比如在生物学中,它可以用来描述种群的增长或衰减;在物理学中,它可以用来计算放射性物质的衰变。
常用对数:生活中的“度量衡”
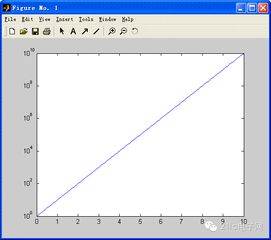
`log10`函数,也就是常用对数,它以10为底。在MATLAB中,计算一个数的常用对数,只需要输入`log10(x)`。比如,你想知道100的常用对数是多少,直接输入`log10(100)`,MATLAB就会告诉你答案是2。
常用对数在日常生活中也很常见,比如在音频处理、地震学等领域,常用对数可以帮助我们更好地理解和处理数据。
以2为底的对数:计算机科学的“密钥”
`log2`函数,也就是以2为底的对数,它在计算机科学中有着非常重要的地位。在MATLAB中,计算一个数的以2为底的对数,只需要输入`log2(x)`。比如,你想知道8的以2为底的对数是多少,直接输入`log2(8)`,MATLAB就会告诉你答案是3。
以2为底的对数与二进制运算紧密相关,因此在计算机科学中有着广泛的应用。
换底公式:数学世界的“万能钥匙”
有时候,你可能需要计算以其他底数为底的对数,这时候,换底公式就能派上用场了。换底公式是:`loga(b) = logc(b) / logc(a)`,其中c是任意正数且不等于1。
在MATLAB中,我们可以通过`log(x, base)`来计算以base为底的对数。比如,你想知道16的以4为底的对数是多少,直接输入`log(16, 4)`,MATLAB就会告诉你答案是2。
换底公式就像一把万能钥匙,可以打开数学世界的大门。
注意事项:小心驶得万年船
在使用对数函数时,需要注意以下几点:
1. 对数函数的定义域是所有正数,即对于`log(x)`,x必须大于0。如果输入值为0或负数,MATLAB会返回一个错误。
2. 对于非常接近0的正数,对数值会非常大,甚至可能超出MATLAB的浮点数表示范围。
3. 在计算对数之前,请确保你的数据是有效的。
:MATLAB对数函数,你的数学好帮手
MATLAB中的对数函数,就像一位默默无闻的助手,它可以帮助你轻松解决各种数学问题。无论是科学研究还是日常生活,对数函数都能为你提供强大的支持。所以,赶快掌握MATLAB对数函数吧,让你的数学之路更加顺畅!
