圆锥体是一个三维几何形状,它的底面是一个圆,而侧面则是一个连续的曲面,从底面圆的边缘向上延伸到一个顶点。圆锥体的侧面在数学上通常被视为一个直角三角形绕其一条直角边旋转一周形成的曲面。
圆锥体的基本属性包括:
1. 底面:底面是一个圆,其半径为圆锥体底面的半径。
2. 顶点:圆锥体的顶点是一个不在底面上的点,它是侧面曲面的最高点。
3. 母线:母线是从圆锥体顶点到底面圆周上任一点的直线段。圆锥体的侧面由无数条母线组成。
4. 高:高是从顶点垂直到底面的线段,它是圆锥体的高度。
5. 斜高:斜高是从顶点到底面圆周上任一点的线段,它连接顶点和底面圆周上的点。
6. 体积:圆锥体的体积可以通过公式 计算,其中 是底面圆的半径, 是圆锥体的高。
7. 表面积:圆锥体的表面积包括底面圆的面积和侧面的面积。底面圆的面积是 ,侧面的面积可以通过公式 计算,其中 是斜高。
圆锥体在几何学、物理学和工程学等领域有广泛的应用。例如,在物理学中,圆锥体的形状可以用来描述光线在通过透镜时的折射和聚焦。在工程学中,圆锥体的形状可以用来设计各种机械部件和结构。你知道吗?在我们周围的世界里,有一种神奇的几何形状,它既神秘又常见,它就是——圆锥体!想象一个尖尖的帽子,或者一个倒置的冰淇淋蛋筒,它们都是圆锥体的化身。那么,什么是圆锥体呢?让我们一起揭开它的神秘面纱吧!
圆锥体的诞生:旋转的魔法

圆锥体,这个名字听起来就充满了魔力。它是由一个圆和一条直线(这条直线叫做母线)共同创造的。具体来说,当你把一个直角三角形拿起来,让它的直角边旋转一圈,那么斜边就会围绕直角边旋转,形成一个圆锥体。这个斜边就是圆锥体的母线,而直角边旋转形成的圆面则是圆锥体的底面。
圆锥体的结构:高、底、母线

圆锥体有三个关键的部分:高、底和母线。
- 高:想象从圆锥体的顶点(也就是直角三角形的顶点)到底面圆心的距离,这就是圆锥体的高。它就像圆锥体的脊梁,支撑着整个形状。
- 底:圆锥体的底面是一个圆,这个圆的半径决定了圆锥体的大小。
- 母线:母线是连接圆锥体顶点和底面圆周上任意一点的线段。它就像圆锥体的裙摆,从顶点到底面展开。
圆锥体的种类:正圆锥与斜圆锥
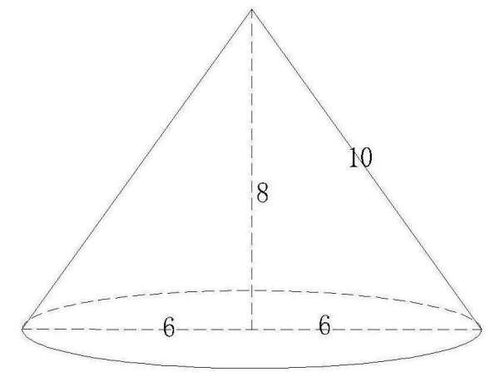
圆锥体并不是千篇一律的,它有几种不同的类型。
- 正圆锥:这种圆锥体的顶点正好位于底面圆心的正上方。想象一个完美的冰淇淋蛋筒,它的顶点就在圆心的正上方,这就是正圆锥。
- 斜圆锥:这种圆锥体的顶点不在底面圆心的正上方。它就像一个倾斜的帽子,顶点偏移了圆心。
圆锥体的应用:无处不在的几何魔法
圆锥体不仅仅存在于我们的想象中,它还广泛应用于我们的生活中。
- 建筑:建筑师们经常使用圆锥体来设计屋顶和烟囱。
- 工程:工程师们利用圆锥体的稳定性来设计桥梁和建筑结构。
- 日常生活:从冰淇淋蛋筒到圣诞帽,从漏斗到铅笔尖,圆锥体无处不在。
圆锥体的计算:数学的奥秘
圆锥体的魅力不仅在于它的形状,还在于它的数学性质。我们可以通过一些简单的公式来计算圆锥体的体积和表面积。
- 体积:圆锥体的体积是底面积乘以高再除以3。简单来说,就是底面圆的面积乘以高,然后分成三份。
- 表面积:圆锥体的表面积包括底面积和侧面积。底面积就是圆的面积,而侧面积则是圆锥侧面展开后的扇形面积。
圆锥体的未来:无限的可能
圆锥体,这个看似简单的几何形状,却蕴含着无限的可能。随着科技的发展,我们可能会发现更多关于圆锥体的奇妙应用。也许,在不久的将来,圆锥体会在我们的生活中扮演更加重要的角色。
所以,下次当你看到圆锥体时,不妨停下脚步,仔细观察它,感受它的魅力。也许,你会在圆锥体的世界里发现一个全新的世界。这就是圆锥体,一个充满魔力的几何形状,一个无处不在的存在。
